[메디컬 세특 칼럼] 로그의 활용 : Log scale
안녕하세요 Recordwriter입니다. 이번 게시글은 수학1 교과 세특 참고자료로 제작한 '로그의 활용 : Log scale' 제목의 세특 칼럼이며 제가 이전에 블로그에 작성한
화학1 완충용액의 원리 : Handerson Hasselbalch Equation과 연관성이 있으므로 필요하시다면 함께 확인하시고 활용하시면 좋을 듯 합니다.
✔️ 과목 : 수학 1
✔️ 학년 : 고2 ~ 고3
✔️ 탐구 주제 : 로그의 활용
1. 탐구 동기
우리는 수학1 교과 수업을 통해 로그가 어떤 것이며, 이를 단순히 계산적인 측면에서 어떻게 처리할 것인지에 대해 집중적으로 배우며 연습하지만 그게 어떤 의미를 가지는 것이며 궁극적으로는 어떻게 활용될 지에 대해서는 생각해본 적이 많지 않다. 지난 탐구에서 완충용액의 원리를 설명하는 Handerson Hasselbalch Equation에 로그가 포함되어 있는 것을 보며 로그라는 수학적 도구가 가지는 실용적 측면에 대하여 그 본질을 탐구해보고 싶은 생각이 들었다.

2. 탐구 내용
① 교과 내용 정리
로그란 어떤 수를 나타내기 위해 고정된 밑을 몇번 곱하여야 하는지를 알려주는 수학적 도구이다. 2를 5번 제곱한 값이 무엇인가?에 대한 답은 지수방정식으로 표현될 수 있는 반면 32는 2를 몇번 곱한 것인가?하는 질문은 로그를 활용해 표현할 수 있다. 이러한 예시에서 우리는 로그와 지수가 역함수의 관계에 있다는 것을 알 수 있다.

로그는 밑과 진수로서 표현되는데, 밑은 1이 아닌 양수여야하며 진수는 항상 양수여야 한다는 조건이 존재한다. 또한 우리는 주로 계산적인 관점에서 로그의 밑과 진수를 어떻게 처리하는지에 대해 주로 배우며 이를 정리하면 아래와 같다.

이처럼 교과 내용을 다시 한번 스스로 정리해보는 것은, 세특에 기재되어야 할 중요한 요소는 아니지만, 해당 탐구가 교과내용의 완전한 이해에서 비롯된 것이며 교과 내용과 큰 관련성을 가진다는 것을 강조하기 위함이다.
② 심화 내용 탐구
로그의 활용적 측면에 대해 복잡하게 파고들기 전에 로그를 취하는 것을 가장 직관적으로 설명해보자. 로그는 큰 수를 간단한 수로 변환 시킨다는 것이 우리에게 가장 와닿는 로그의 본질적 특성이며 이것이 로그 활용의 기본이 된다.
A~D라는 4명의 사람이 각각 100만원, 1억원, 10억원, 12억원이라는 돈을 가지고 있다고 가정해 보자.
✔️ A : 100 만원
✔️ B : 1 억원
✔️ C : 10 억원
✔️ D : 12 억원
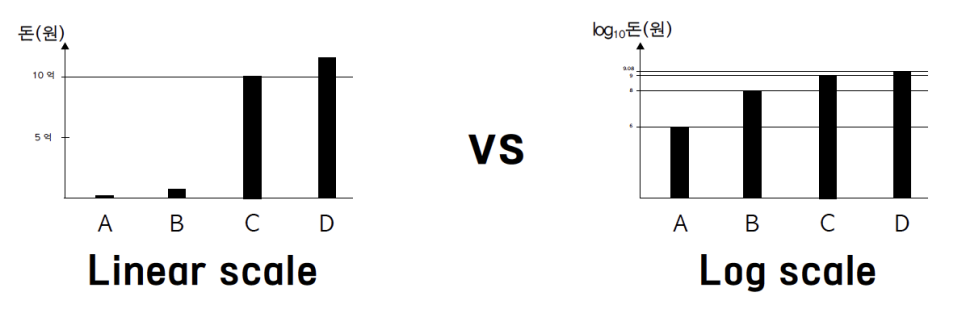
이들이 가진 돈을 하나의 그래프로 표현하고 그 관계에 대해 설명할 수 있을까? 이 과정에서 우리가 당장에 직면하는 문제점은 이처럼 큰 차이를 가지는 수들을 하나의 눈금체계(하나의 축)로 표현하기가 쉽지 않다는 것이다. 그럼에도 축을 지나치게 늘려 어떻게든 하나의 그래프상에 아래와 같이 나타내었다고 하자.
우리가 표나 그래프와 같은 도구를 활용하는 것은 수로 표현되는 데이터를 보다 시각적으로 나타내어 그 관계를 이해하기 쉽게 하기 위해서다. 위 그래프는 그러한 목적에 부합하는가? 이러한 관점에서 두가지 문제를 제기할 수 있다.
문제 ①
100만원(A)과 12억(D)이라는 큰 차이를 가지는 수를 하나의 축 하에 표현하기 위해 축을 지나치게 늘렸고 그 결과 비교적 작은 값인 A와 B는 그래프 상에서 시각적으로 정확히 표현되기가 어렵다.
문제 ②
A와 B는 절대적 금액의 값 차이가 9900만원인 반면 C와 D의 차이는 그 2배 이상인 2억에 해당한다. 이러한 차이는 그래프 상에서 막대의 높이 차이로 그대로 반영되어 나타나는데, 그렇다면 우리는 D는 C보다 훨씬 부자인 반면, A와 B는 재산의 차이가 비교적 적은 것이라 할 수 있는가?
현실적인 관점에서 100만원 하던 주식이 1억원이 된다면 우리는 이를 '대박'이라 표현할 것이다. 분명 이는 10억원이 12억원이 되는 것보다 체감적으로 더 크게 느껴지는 것이지만 절대 값으로 표현된 선형 그래프는 이를 잘 표현하지 못한다.
로그 활용의 실용적 도구
: Log scale
앞서 살펴본 문제의 본질적 원인은, 우리가 비율적 차이보다는 절댓값의 차이로 그래프를 표현하였기 때문이다.
하지만 앞선 예시와 같이 우리의 생활 중에는 절댓값의 차이보다 비율적인 변화가 더 중요한 상황들이 더러 있다. 이러한 문제를 해결하기 위해 우리는 축을 지나치게 늘리는 대신, y축에 밑이 10인 상용로그를 취하는 방식을 취할 수 있다.

y축에 상용로그를 취한 이 그래프는 이전 그래프와 어떤 차이가 있는가? 우선 절대적으로 큰 차이를 가지는 값들을 하나의 축 상에서 적당한 값으로서 나타낼 수 있다. 이는 로그를 취함으로서 큰 값들을 간단한 작은 값들로 변환하였기에 가능한 것이다.
또한, 해당 그래프는 A와 B의 재산 차이가 C와 D의 재산 차이보다 비율적으로 더 크다는 것을 명확히 보여준다. 즉, 로그를 취하는 것은 절대적 값의 차이를 비율적 차이로 전환시키는 것이며 이는 그래프를 통한 보다 직관적 이해를 가능하게 한다.


앞선 그래프 표현 방식을 Linear scale(선형스케일)이라 하며 이는 우리에게 보다 친숙한 방식이다. 반면 축에 log를 취하여 표현하는 방식을 Log scale이라 하는데 이는 값들 사이의 비율적 관계를 명확하게 나타낸다.
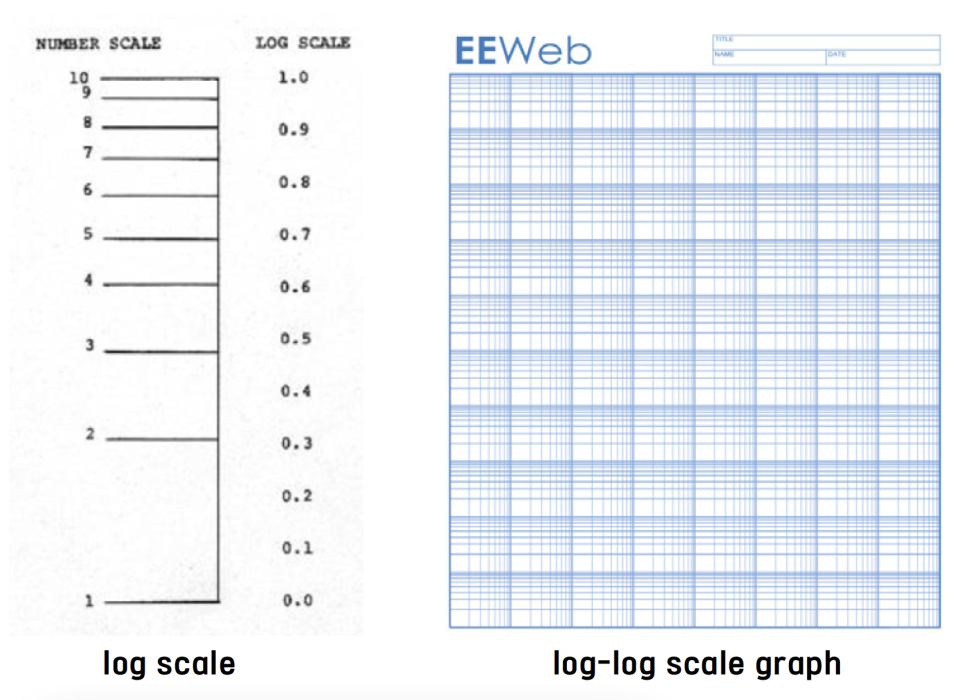
Log scale은 x축과 y축 중 하나에만 로그를 취하여 그래프로 표현하는 semi-log graph, 혹은 x축과 y축 모두에 로그를 취해 표현하는 log-log graph 로 활용되며 이러한 그래프 방식은 자연 과학, 공학 등 여러 과학 분야에서 광범위하게 활용되고 있다.
< log scale의 장점 정리하기 >

3. 진로 연계
앞서 살펴본 것처럼 로그로 표현하는 방식은 다양한 장점을 지니며 따라서 우리 주변의 많은 분야에서 활용되고 있다.

가장 대표적인 예시는 완충용액을 설계하는 과정에서 완충용액의 원리를 설명하는 Handerson-Hasselbalch Equation에 로그가 포함된 것이며 이는 지난 탐구 게시글을 참고하도록 합시다!
https://blog.naver.com/c1c23c/222975086035
4. 결론

텍스트 복사가 가능한 PDF 파일은 아래 블로그를 통해 무료로 다운로드 가능합니다! 감사합니다.
https://blog.naver.com/c1c23c/222979643094
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
팁같은게 있을까요... 꾸역꾸역 스타트를 끊긴 했는데 계속 생각이 멈춰서요 ㅜㅜㅜ
-
과거 못바꾸고 살아온 인생 그대로 다시 살아와야됨
-
씨발ㅠㅠ
-
ㅈ오오오오온나 재밌음,,,,ㄷㄷ
-
미친새끼 3일 내로 온다면서 드럽게 안오고 워크북 같이 안 시킨 걸 존나 후회함뇨...
-
새해됐다고 업데이트된듯
-
누구일까
-
그래서 종종 이상한 글인데 좋아요를 눌러버림
-
https://ratio.uwayapply.com/Sl5KOTpWcldhVkpyVzovSiNmVGY
-
점공 ㅇㅈ 5
가. 경북대 컴퓨터학부 2025는 최초합 확정이라서 안돌림 ㅇㅅㅇ 나. 경희대...
-
슨상님... 1
?
-
여기서만이라도 인싸가 되고싶다
-
걍 보면 cc도 엥 국어 한문제 맞으면 되는거 아님 이래도 한문제 한문제가 진심...
-
24수능 현장에서 미적29번 풀이 시작했는데 12시 9분에 딱 초침 도착하는걸...
-
셋 중 하나라도 다녀보신 분들 후기 좀 부탁드립니다ㅜㅜ (센텀점이면 좋겠지만...
-
ㄹㅇ...
-
정시황의 심판을 받겠읍니다
-
아무거나 올려주시면….. 성실히… 답변을…. 해드리겠습니다….
-
올만에 맞팔구 21
-
음 0명이었으면 좋겠어
-
걱정부터 앞서기 시작함 강민철을 들어본 경험은 솔직히 없는데 주변 4등급 이하...
-
이십대 초중반은 나에겐 없는 기억이네
-
글캠 다닐땐 1시간 30분은 껌이었는데 시골로 가는거라 사람이 없어서 그렇게...
-
무물보 받겟습니다 18
자취 예정이구요 과제가 산더미처럼 잇습니다 피부과가서 압출하고 왓더니 너무 아팟어요...
-
점공상 2배수 점수차이가 20점 미만인데 cc면 정확히 3점 깎인다고 생각하면...
-
점심시간 답 맞췄는데 22번 케이스 누락을 발견했을때
-
다군 70명뽑는데최종업뎃은 100등이엇고 막판에 실지원자는 90등이엇요 점공에선...
-
국어 기간맞춰 정석민 풀커리, 화작총론, 화작 마더텅, 수특수완 독서 사용설명서,...
-
다들 그런 반응이길래... 근데 아주 많은 뜻?이 있는 닉네임이긴 해요!!
-
과학고 조기졸업했고, 2-1까진 잘 나오다가 2-2때 수시 안들어간다고...
-
대학 물리랑 많이 달르드라.. 특히 비역학 파트는 아예 다름..
-
저 혼자 만점이고 2등은 8n점인 시험도 있었음 그냥 유일무이 사문황이었는데 수능만 치면 제일 망함
-
흐흐흐 또르비해 이럼
-
국어: 강기본(거의 완강), 강기분 독서문학화작, 개념의 나비효과 수학: 시발점...
-
고정 1이 없어 3
한국사 빼고 없어 예측이란 게 도무지 가능하지 않은 나의 변화무쌍한 브레인아
-
비정상인가...? 동생도 타지 갈 거고 (수원) 그런데 왜 기분이 좀...
-
대학교 수업료도 이따구는 아닌데… 수능 허접이라 장학을 얼마 못받을거 같아서 울었어….
-
고딩때 한문선생 보니까 진짜 놀고 먹어도 월급 꽂히는 개꿀직업 이긴함 3
농담아니라 고딩때 한문센세 진도는 안나가고 맨날 노트북 가져와서 게임하고 대놓고...
-
그때 며칠동안 무등비 꿈만 꿧엇음 애들한테 말하니깐 호들갑떨지 말라그랫는데 난...
-
3떨 할 확률 0.342225 나는 0.657775의 확률로 대학에 간다
-
친구 앞에서 오르비하기 11
에휴
-
카리나랑 데이트하기vs 20
정벽 특정하기
-
누가 더 능지 높음뇨?
-
과기대를 찾아 보세요
-
한양 1
한양대 진학사 점공 표본이 너무 적은거 같아요 ㅠㅠ 더 떨어질까 두렵네요..
-
과기원 반도체 1
정시로 어디랑 입결 겹치나요
-
절 응원해주세요 히이잉
-
사탐특이 10
다 맞은거 같은데 채점하면 ㅈㄴ틀림 근데 이래도 과학보다 등급 잘나옴
-
시골 왔다뇨





























































첫번째 댓글의 주인공이 되어보세요.